SVM: Difference Between Linear and Non-Linear Models

Support Vector Machines (SVM) are widely used in machine learning for classification and regression tasks. Their ability to handle high-dimensional data and maintain robustness against overfitting makes them a preferred choice for many applications, such as image recognition, bioinformatics, and text classification. However, understanding the difference between linear and non-linear SVM models is crucial for choosing the right approach.

According to IBM, SVMs are applied in various AI-based classification tasks, demonstrating their effectiveness in machine learning applications.

In this article, we will explore what linear and non-linear SVMs are, how they work, and how to choose between them. We will also discuss the kernel trick, an essential concept in non-linear SVMs.

What is a Linear SVM?

A linear (Support Vector Machines) SVM is a type of SVM used when the dataset is linearly separable, meaning the data points can be divided by a straight line (in two dimensions) or a hyperplane (in higher dimensions).

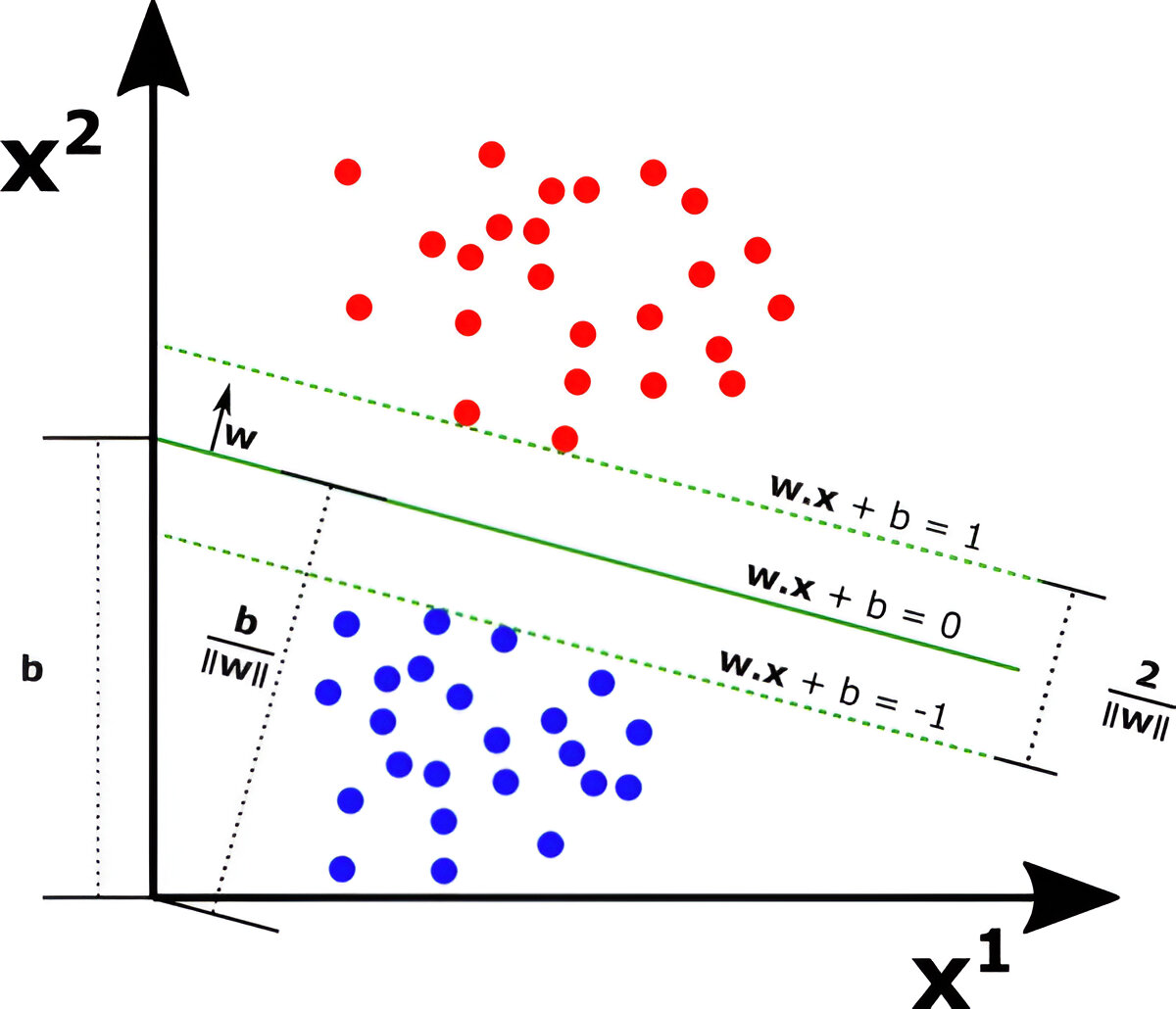
Example of Linearly Separable Data

Consider a dataset where red and blue points can be separated by a straight line. This is an example of a linearly separable dataset, where SVM finds the optimal hyperplane that maximizes the margin between the two classes.

Mathematical Representation:

A hyperplane in an n-dimensional space is represented as:

 

where:

• w = Weight vector
• x = Input feature vector
• b = Bias term

A linear SVM aims to find the optimal w and b such that the margin between the nearest data points of each class (support vectors) is maximized.

How to Find the Right Hyperplane (Linear Data)?

Finding the optimal hyperplane involves:

1. Maximizing the Margin: The goal of an SVM is to maximize the distance between the hyperplane and the nearest data points (support vectors).
2. Using the Support Vectors: These are the critical data points that define the decision boundary.
3. Mathematical Optimization: The SVM solves the following convex optimization problem:

    

   Subject to:

    

where represents class labels (+1 or -1).

According to PubMed Central, SVM models with optimized hyperplanes improve classification accuracy by 10-15% compared to non-optimized models.

What is a Non-Linear SVM?

A non-linear SVM is used when the dataset is not linearly separable. In real-world applications, most datasets are complex and cannot be separated by a straight line.

Example of Non-Linearly Separable Data

Consider a dataset where red and blue points form concentric circles. A straight line cannot separate them; thus, we need a non-linear decision boundary.

Key Differences Between Linear and Non-Linear SVM

Feature	Linear SVM	Non-Linear SVM
Data Separability	Works on linearly separable data	Handles complex, non-linear data
Decision Boundary	Straight line (or hyperplane)	Complex, curved decision boundary
Kernel Trick Usage	Not required	Required
Computational Complexity	Lower	Higher (due to kernel computation)
Examples	Spam detection, fraud detection	Image recognition, speech processing

A study from ResearchGate indicates that non-linear SVMs improve classification accuracy by up to 20% in complex datasets compared to linear models.

The Kernel Trick in Non-Linear SVM

The kernel trick allows SVM to transform data into a higher-dimensional space, where it becomes linearly separable. Instead of explicitly transforming the data, SVMs use kernel functions to compute inner products in the transformed space efficiently.

Popular Kernel Functions

1. Polynomial Kernel: Handles curved decision boundaries
2. Radial Basis Function (RBF) Kernel: Captures complex patterns
3. Sigmoid Kernel: Used in neural networks

When to Use Linear vs. Non-Linear SVM?

Use Linear SVM When:

• The dataset is linearly separable.
• You need a simpler and faster model.
• Computational resources are limited.

Use Non-Linear SVM When:

• The dataset is complex and non-linearly separable.
• The problem requires higher accuracy.
• You can afford higher computational costs.

According to a Google AI report, using an RBF kernel in non-linear SVMs improves classification performance in tasks like image classification and text sentiment analysis.

Conclusion

Choosing between a linear and non-linear SVM depends on the dataset’s nature. If the data is linearly separable, a linear SVM is a fast and efficient choice. However, for complex data with non-linear patterns, kernel-based SVMs offer higher accuracy at the cost of increased computational complexity.

By understanding the differences and use cases of linear vs. non-linear SVMs, you can make informed decisions for your machine learning models and improve their performance significantly.